[DSA T6 2024]. TEST 3. STRING, SET, MAP
[Set & Map]. Bài 28. Tần suất lớn nhất
Nộp bàiPoint: 1
Cho mảng A[] gồm N kí tự, bạn hãy xác định xem tần suất lớn nhất của 1 kí tự xuất hiện trong mảng là bao nhiêu. Và có bao nhiêu kí tự thỏa mãn có tần suất lớn nhất đó. Ví dụ : A[] = {2, 8, t, e, c, h, t, e, c, h} thì tần suất lớn nhất của 1 kí tự lớn nhất là 2 và có 4 kí tự t, e, c, h thỏa mãn
Đầu vào
Dòng 1 là N : số kí tự trong mảng
Dòng 2 gồm N kí tự viết cách nhau 1 dấu cách
Giới hạn
1<=N<=10^6
Các kí tự là chữ in hoa, in thường và chữ số
Đầu ra
Dòng 1 in ra tần suất lớn nhất của kí tự
Dòng 2 in lần lượt các kí tự thỏa mãn có cùng tần suất lớn nhất đó theo thứ tự từ điển tăng dần.
Ví dụ :
Input 01
10
2 8 t e c h t e c h
Output 01
2
c e h t
[Set & Map]. Bài 29. Kí tự chữ cái khác nhau
Nộp bàiPoint: 1
Cho một mảng kí tự A[] gồm N kí tự, bạn hãy xác định có bao nhiêu kí tự là chữ cái khác nhau xuất hiện trong mảng A[] nhưng không phân biệt hoa thường. Tức là chữ cái in hoa và in thường của cùng 1 chữ cái được coi là giống nhau, ví dụ a và A được coi là giống nhau.
Đầu vào
Dòng 1 là N : số kí tự trong mảng
Dòng 2 gồm N kí tự viết cách nhau 1 dấu cách
Giới hạn
1<=N<=10^6
Các kí tự là chữ in hoa, in thường và chữ số
Đầu ra
Dòng 1 in ra số lượng kí tự chữ cái khác nhau
Dòng 2 liệt kê các chữ cái khác nhau đó theo thứ tự từ điển tăng dần.
Ví dụ :
Input 01
10
2 8 T E C H t e c h
Output 01
4
c e h t
[Set & Map]. Bài 30. Tần suất số đẹp
Nộp bàiPoint: 1
Cho mảng A[] gồm N số nguyên, số đẹp là số chỉ bao gồm các chữ số 0, 2, 6, 8 theo quan niệm của 28Tech. Bây giờ bạn cần đếm xem mỗi số đẹp trong mảng A[] xuất hiện bao nhiêu lần và liệt kê theo thứ tự xuất hiện trong mảng.
Đầu vào
Dòng 1 là N : số lượng phần tử trong mảng
Dòng 2 gồm N số trong mảng A[]
Giới hạn
1<=N<=10^5
0<=A[i]<=10^18
Đầu ra
In ra các số đẹp xuất hiện trong mảng A[] kèm theo tần suất của nó
Ví dụ :
Input 01
6
22 66 88 22 11 3
Output 01
22 2
66 1
88 1
[Xâu Ký Tự]. Bài 62. Tìm kiếm trong đám đông
Nộp bàiPoint: 1
Một đám đông được xếp thành N hàng, mỗi hàng có 1 số người nhất định. Nhiệm vụ của bạn là hãy tìm tên người đứng ở số thứ tự y trong hàng x.
Ví dụ người đứng ở hàng 3 số thứ tự 5 có tên là X
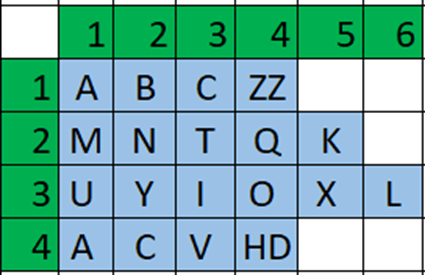
Đầu vào
Dòng 1 là N và Q tương ứng với số hàng của đám đông và số truy vấn
N dòng tiếp theo mỗi dòng mô tả 1 hàng người, trong đó số đầu tiên của 1 dòng là số người có trong hàng đó gọi là M, M từ tiếp theo là tên của M người trong hàng, tên người chỉ bao gồm 1 từ.
Q dòng tiếp theo mỗi dòng là 2 số x, y tương ứng với truy vấn
Giới hạn
1<=N,M<=10^5
1<=Q<=1000
1<=x<=N
y đảm bảo là số thứ tự phù hợp với từng hàng
Đầu ra
In ra tên người của mỗi truy vấn trên từng dòng
Ví dụ :
Input 01
8 9
5 Biden Hanh Elon Ngoc Duc
12 Hanh Biden Thuy Thuy Duc Tim Biden Thuy Tim Lan Elon Nhung
10 Ngoc Phuong Duc Ngoc Hanh Duc Phuong Tim Lan Lan
10 Nhung Lan Ngoc Ngoc Biden Phuong Nhung Elon Phuong Duc
7 Lan Elon Lan Tim Biden Ngoc Elon
7 Phuong Hanh Lan Tim Hanh Elon Duc
10 Hanh Hanh Biden Duc Nhung Duc Tim Elon Lan Thuy
14 Biden Hanh Lan Duc Phuong Thuy Thuy Thuy Thuy Nhung Biden Lan Phuong Hanh
4 10
4 9
2 5
7 7
1 4
4 3
1 1
4 7
4 3
Output 01
Duc
Phuong
Duc
Tim
Ngoc
Ngoc
Biden
Nhung
Ngoc
[Xâu Ký Tự]. Bài 63. Xâu ký tự BTC
Nộp bàiPoint: 1
28Tech rất thích BTC và bây giờ anh ta nhờ bạn giúp 1 bài toán, nếu làm đúng bạn sẽ nhận được 1 BTC tương đương khoảng 64K đô la tại tháng 4/2024. Bài toán như sau : Cho xâu S có độ dài N chỉ bao gồm 3 chữ cái là B, T, C trong đó có ít nhất b chữ B, ít nhất t chữ T, ít nhất c chữ C, bạn hãy xác định có thể tồn tại bao nhiêu xâu S.
Gợi ý : Dùng vòng for lồng nhau để xét được mọi cặp thỏa mãn phương trình x + y + z = N với x >= b, y >= t và z >= c.
Bài này các bạn sử dụng kiến thức về Multinomial Coefficient. Ví dụ bài toán là cho từ mississippi, hỏi có bao nhiêu từ khác nhau có thể tạo thành bằng cách sắp đặt lại các kí tự trong từ này. Nó tương tự như đếm số cách chia n phần tử thành các tập có k1, k2, k3…km phần tử.

Ví dụ N = 4, b = 1, t = 1, c = 1 thì có tất cả 36 xâu thỏa mãn đó chính là b = 2, t = 1, c = 1 có 4! / (2! * 1! * 1!) = 12 cách b = 1, t = 2, c = 1 có 4! / (2! * 1! * 1!) = 12 cách b = 1, t = 1, c = 2 có 4! / (2! * 1! * 1!) = 12 cách
Đầu vào
Dòng 1 là T : số test case
T dòng tiếp theo mỗi dòng là 1 test gồm 4 số N, b, t, c
Giới hạn
1<=T<=1000
1<=N<=20
1<=b,t,c<=N
Đầu ra
In ra kết quả của mỗi test trên từng dòng
Ví dụ :
Input 01
5
15 4 2 1
15 6 5 3
17 3 1 7
17 1 1 11
16 6 1 6
Output 01
11043461
1411410
37925606
990624
5102240
[Xâu Ký Tự]. Bài 64. Xâu chia hết
Nộp bàiPoint: 1
Cho xâu ký tự S gồm các chữ số từ 0 tới 9, bạn hãy đếm số lượng xâu con liên tiếp chia hết cho 8 mà không chia hết cho 3.
Gợi ý : Dùng 2 vòng for lồng nhau để xét tất cả các xâu con, với mỗi xâu con thì tìm số dư của xâu con này vs X để xác định xem nó có chia hết cho X hay không. Lý thuyết này có ở bài tập phép chia dư Chia dư số nguyên lớn với 1 số nguyên
Bây giờ bạn chỉ cần đếm số xâu con chia hết cho 8 - số xâu con chia hết cho 24 là ra số xâu con chia hết cho 8 nhưng không chia hết cho 3.
Đầu vào
Dòng 1 là T : số test case
T dòng tiếp theo mỗi dòng là 1 test gồm xâu S
Giới hạn
1<=T<=100
S có không quá 500 chữ số
Đầu ra
In ra kết quả của mỗi test trên từng dòng
Ví dụ :
Input 01
5
9824640
13198
9412690602
5893653
25524773029
Output 01
10
1
0
3
1