[DSA T7 2024]. TEST 4. MẢNG 2 CHIỀU
[Mảng 2 Chiều]. Bài 36. Perfect garden
Nộp bàiPoint: 100
28Tech có một mảnh vườn do ông cha để lại, anh ta quy hoạch mảnh vườn thành các ô vuông nhỏ rất đẹp. Khi quy hoạch xong anh ta thấy mảnh vường có tất cả N hàng và mỗi hàng gồm M ô vuông nhỏ. Mỗi ô vuông anh ta trồng một cây cà rốt, có những ô anh ta bỏ trống. Là một người thích sự hoàn hảo, anh ta yêu thích các mảnh vườn nhỏ liền kề nhau (những ô vuông nhỏ chung đỉnh sẽ thuộc về cùng 1 mảnh vườn nhỏ) mà trồng toàn cà rốt nhưng mảnh vườn nhỏ này nhất định phải có hình dạng là một hình chữ nhật. Bạn hãy giúp anh ta đếm xem có bao nhiêu mảnh vườn nhỏ chứa toàn cà rốt mà lại có hình dạng hình chữ nhật nhé. Ví dụ mảnh vườn sau sẽ có 2 mảnh vườn nhỏ HCN :
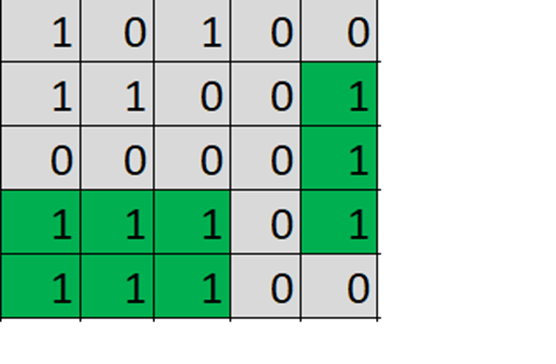
Gợi ý : Loang rồi tìm diện tích từng khu vườn nhỏ, xác định dòng đầu tiên, dòng cuối cùng, cột đầu tiên, cột cuối cùng của HCN đó thông qua tọa độ từng ô trên khu vườn nhỏ. So sánh diện tích tính theo cách tính của HCN vs diện tích đếm được khi loang.
Đầu vào
• Dòng 1 gồm N và M
• N dòng tiếp theo mỗi dòng chứa M số 0 hoặc 1, 0 tương ứng với ô trống, 1 tương ứng với ô trồng cà rốt.
Giới hạn
• 1<=N,M<=100
• 0<=A[i][j]<=1
Đầu ra
In ra số mảnh vườn thỏa mãn
Ví dụ :
Input 01
5 7
0 1 0 1 0 1 0
0 0 0 1 0 0 0
1 1 0 0 0 0 1
0 0 0 0 0 0 1
1 1 0 0 0 1 0
Output 01
5
[Mảng 2 Chiều]. Bài 37. Gieo hạt
Nộp bàiPoint: 100
28Tech đang gieo hạt giống trên khu vườn ông hình chứ nhật cha anh ta để lại. Mảnh vườn này có N luống ngang, mỗi luống ngang sẽ chia thành M ô vuông nhỏ để gieo hạt. 28Tech sử dụng một robot để gieo những hạt giống, robot này thì tương đối kém thông minh vì thế nó chỉ có thể gieo hạt 1 loạt các ô trong hình chữ nhật với ô trên bên trái là ô (1, 1) và ô dưới bên phải của hình chữ nhật là ô (x, y).
Ví dụ khi 28Tech nhập tọa độ (x, y) lập tức robot sẽ gieo hạt vào mọi ô trong hình chữ nhật có ô góc dưới bên phải bằng 1 hạt giống. Ví dụ về việc robot gieo hạt khi nhận tọa độ gieo hạt là (5, 6) : 28Tech đang gieo hạt giống trên khu vườn ông hình chứ nhật cha anh ta để lại. Mảnh vườn này có N luống ngang, mỗi luống ngang sẽ chia thành M ô vuông nhỏ để gieo hạt. 28Tech sử dụng một robot để gieo những hạt giống, robot này thì tương đối kém thông minh vì thế nó chỉ có thể gieo hạt 1 loạt các ô trong hình chữ nhật với ô trên bên trái là ô (1, 1) và ô dưới bên phải của hình chữ nhật là ô (x, y).
Ví dụ khi 28Tech nhập tọa độ (x, y) lập tức robot sẽ gieo hạt vào mọi ô trong hình chữ nhật có ô góc dưới bên phải bằng 1 hạt giống. Ví dụ về việc robot gieo hạt khi nhận tọa độ gieo hạt là (5, 6) :
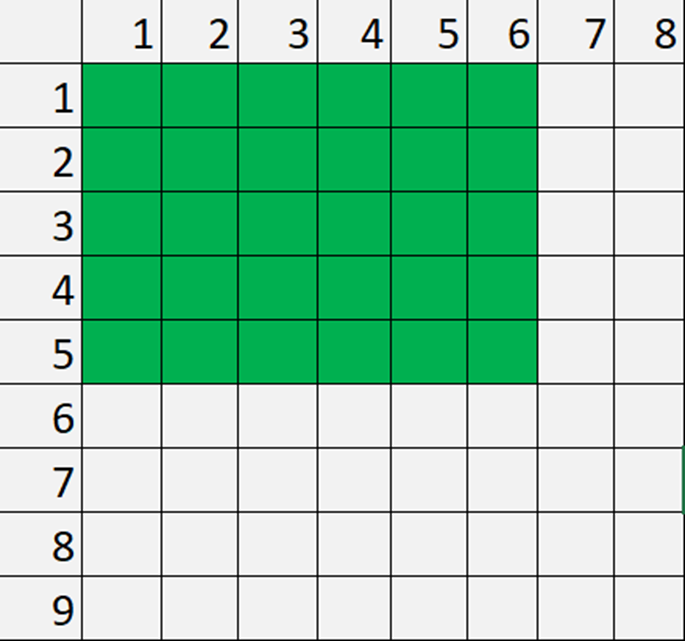
Bây giờ bạn có danh sách T lệnh mà 28Tech nhập cho robot, bạn hãy xác định số ô có nhiều hạt giống nhất
Đầu vào
• Dòng 1 gồm N, M, T
• T dòng tiếp theo mỗi dòng gồm 2 số x, y là tọa độ
Giới hạn
• 2<=N,M<=1000
• 1<=T<=10000
• 1<=x<=N, 1<=y<=M
Đầu ra
In ra đáp án của bài toán
Ví dụ :
Input 01
9 6 4
4 3
5 1
3 1
6 5
Output 01
3
[Mảng 2 Chiều]. Bài 38. Flood fill
Nộp bàiPoint: 100
Cho một bảng số cỡ N hàng và M cột, trên mỗi ô của bảng số có ghi một số nguyên X, Tèo yêu thích các ô trên bảng có cùng giá trị X và nằm cạnh nhau vì thế anh ta nhờ bạn xác định các ô cạnh nhau (chung đỉnh) mà có cùng số ghi trên đó. Tèo coi diện tích một vùng các ô liền kề là số lượng các ô nằm cạnh nhau (chung đỉnh) mà chúng có cùng giá trị của X.
Bạn hãy giúp Tèo liệt kê các giá trị khác nhau xuất hiện trên bảng số theo thứ tự tăng dần và với mỗi giá trị đó bạn hãy liệt kê diện tích các vùng chứa giá trị này theo diện tích tăng dần.
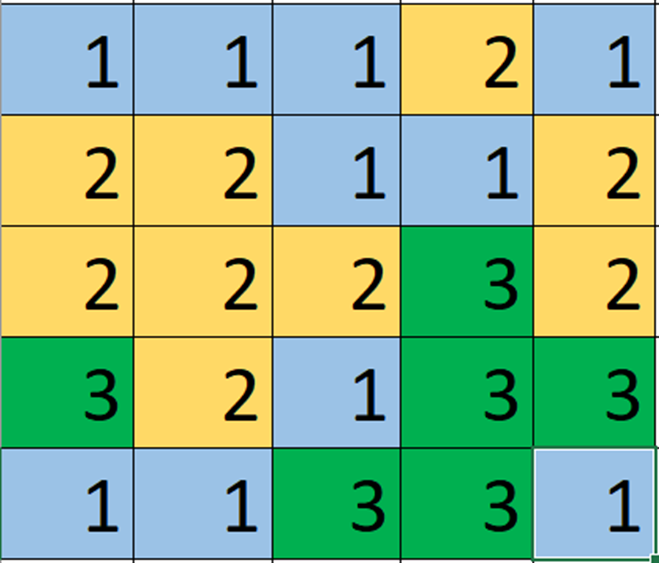
Ví dụ trong hình trên có :
• 3 vùng số 1 với diện tích là 1, 3, 6
• 2 vùng số 2 với diện tích là 3, 6
• 2 vùng số 3 với diện tích là 1, 5
Đầu vào
• Dòng 1 là N và M
• N dòng tiếp theo mỗi dòng gồm M số nguyên X
Giới hạn
• 1<=N,M<=50
• -100<=X<=100
Đầu ra
In ra đáp án của bài toán, với mỗi dòng in ra giá trị và diện tích các cùng chứa giá trị này theo thứ tự tăng dần
Ví dụ :
Input 01
5 5
2 4 3 1 3
4 3 4 1 3
2 3 2 3 3
3 1 4 1 4
2 1 4 3 2
Output 01
1 : 1 2 2
2 : 1 1 1 1 1
3 : 1 4 4
4 : 1 2 3
[Mảng 2 Chiều]. Bài 39. Đếm đường đi
Nộp bàiPoint: 100
Cho ma trận cỡ NxM gồm N hàng, mỗi hàng M cột. Mỗi ô trên ma trận có giá trị là 1 hoặc 0, 1 tương ứng với đường đi và 0 tương ứng với vật cản.
Hãy đếm số cách đi từ ô (1, 1) tới ô (N, M) biết rằng ở mỗi bước đi bạn chỉ có thể đi vào ô không có vật cản nằm bên dưới hoặc bên phải ô hiện tại. Dữ liệu đảm bảo kết quả nằm trong giới hạn của số nguyên 64 bit.
Đầu vào
Dòng đầu tiên là 2 số N và M. N dòng tiếp theo mỗi dòng có M số.
Giới hạn
1≤N,M≤100
0<=A[i][j]<=1
Đầu ra
In ra đáp án của bài toán
Ví dụ :
Input 01
3 3
1 1 1
1 0 1
1 1 1
Output 01
2
[Mảng 2 Chiều]. Bài 40. Set 28
Nộp bàiPoint: 100
Cho ma trận A[][] cỡ NxM gồm N hàng, mỗi hàng M cột. Nhiệm vụ của bạn là hãy cho tất cả các phần tử thuộc hàng I và cột J của ô (I, J) thành số 28 nếu ô A[i][j] = 28.
Đầu vào
Dòng đầu tiên là 2 số N và M.
N dòng tiếp theo mỗi dòng có M số.
Giới hạn
1≤N,M≤1000
0<=A[i][j]<=1000
Đầu ra
In ra ma trận sau khi thay đổi
Ví dụ :
Input 01
5 6
4 1 1 3 3 4
1 7 3 2 6 6
7 8 3 6 6 3
3 4 28 28 7 1
9 9 7 5 8 8
Output 01
4 1 28 28 3 4
1 7 28 28 6 6
7 8 28 28 6 3
28 28 28 28 28 28
9 9 28 28 8 8