Cho một ma trận nhị phân cỡ N x N, bạn xuất phát từ ô (1,1) và tìm đường đi tới ô (N, N). Ở mỗi bước đi bạn được phép đi theo 4 ước trên, dưới, trái, phải của ô hiện tại.

Mỗi lần đi qua một ô bạn sẽ nhặt số 0 hoặc 1 ở ô đó để ghép thành số nhị phân.

Có thể hiểu đơn giản là mỗi đường đi từ ô (1, 1) tới ô (N, N) sẽ tạo ra 1 số nhị phân tương ứng với đường đi đó.

Bạn hãy in ra đường đi có số nhị phân là lớn nhất (dạng thập phân tương ứng của nó là lớn nhất), biết rằng mỗi đường đi bạn chỉ được đi qua mỗi ô 1 lần. Lưu ý rằng các số nhị phân có thể có đường đi với số bit khác nhau.

Đầu vào

• Dòng 1 là số nguyên dương N

• N dòng tiếp theo là ma trận

Giới hạn

• 1<=N<=6

Đầu ra

In ra đường đi tương ứng với số nhị phân lớn nhất.

Ví dụ :

Input 01

3
1 1 1 
1 0 0 
1 0 0

Output 01

111001100

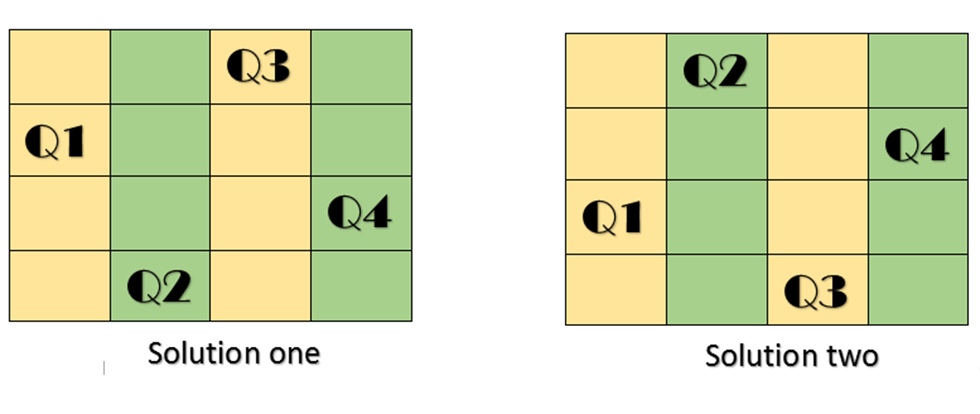
Cho bàn cờ vua cỡ NxN, bạn hãy tìm cách đặt N con hậu vào bàn cờ này sao cho không có 2 con hậu ăn nhau.

Giả sử X1, X2, X3…XN là vị trí con hậu đặt ở hàng 1, 2, 3…N.

Bạn hãy liệt kê các cấu hình này theo thứ tự từ điển tăng dần.

Đầu vào

• Dòng duy nhất chứa N

Giới hạn

In ra các cách đặt thỏa mãn

Đầu ra

In ra các cách đặt thỏa mãn

Ví dụ :

Input 01

4

Output 01

2 4 1 3 
3 1 4 2

Cho một số nguyên dương N, bạn hãy liệt kê các cách phân tích N dưới dạng tổng của các số nguyên dương không vượt quá N.

Các cấu hình được liệt kê theo thứ tự từ điển tăng dần.

Đầu vào

• Dòng duy nhất chứa N

Giới hạn

• 1<=N<=16

Đầu ra

In ra các cách phân tích thỏa mãn

Ví dụ :

Input 01

4

Output 01

1 + 1 + 1 + 1
1 + 1 + 2
1 + 2 + 1
1 + 3
2 + 1 + 1
2 + 2
3 + 1
4

Một con ếch đang đứng ở chỉ số 0 của mảng A[], giả sử con ếch đang ở chỉ số i của mảng A[] thì ở mỗi lần di chuyển nó có thể nhảy sang phải với số bước nhảy lớn nhất bằng với A[i], mỗi bước nhảy sẽ giúp con ếch di chuyển sang phải 1 vị trí trong mảng A[]. Giả sử A[i] = 5 thì từ chỉ số i con ếch có thể nhảy sang phải tối đa 5 vị trí. Bạn hãy xác định xem con ếch có thể di chuyển tới phần tử cuối cùng trong mảng A[] được hay không?

Ví dụ A[] = [1, 3, 2, 2, 0, 0] thì con ếch có thể di chuyển qua các chỉ số như sau : 0->1-> 3->5

Gợi ý : Ở mỗi vị trí I xem từ đó nhảy xa nhất là bao nhiêu, nếu tại 1 vị trí bất kỳ mà nhảy được tới N - 1 thì có thể kết luận ngay.

Đầu vào

Dòng 1 là N : số lượng phần tử trong mảng A[]

Dòng 2 là các phần tử trong mảng A[]

Giới hạn

1<=N<=10^6

0<=A[i]<=10^3

Đầu ra

In ra 28tech nếu con ếch có thể đến được vị trí cuối cùng, 29tech nếu không thể.

Ví dụ :

Input 01

6
1 3 2 2 0 0

Output 01

28tech

28Tech đang có một chiến lược mua bitcoin, may mắn là anh ta biết trước giá của bitcoin trong N ngày liên tiếp luôn rồi nhưng không may là anh ta không biết ngày nào mua ngày nào bán để kiếm được lợi nhuận lớn nhất sau N ngày. Ở mỗi ngày anh ta có thể mua, bán hoặc không mua bán gì cả. Tuy nhiên ở mỗi ngày anh ta nếu đang giữ bitcoin mua ở 1 ngày nào trước đó rồi thì anh ta không được mua thêm nữa mà chỉ có thể bán hoặc giữ. Tất nhiên anh ta chỉ có thể bán vào những ngày sau ngày mua.

Bạn hãy giúp 28Tech tìm ra lợi nhuận lớn nhất có thể nhé.

Ví dụ giá bitcoin trong N ngày sẽ là [1, 3, 6, 3, 2, 4, 5, 7, 6, 1] thì anh ta sẽ mua ở ngày 1, bán ở ngày 3 lợi nhuận thu được là 5, tiếp tục mua bitcoin ở ngày thứ 5 và bán ở ngày thứ 8 lợi nhuận thu được là 5. Vậy tổng lợi nhuận lớn nhất thu được là 10. Ngày thứ 9, 10 thấy giá giảm nên sẽ không mua.

Đầu vào

Dòng 1 là N : số ngày

Dòng 2 là N số tương ứng với giá bitcoin trong N ngày

Giới hạn

1<=N<=10^6

0<=A[i]<=10^9

Đầu ra

In ra lợi nhuận lớn nhất mà 28Tech có thể kiếm được.

Ví dụ :

Input 01

6
1 6 7 9 2 3

Output 01

9