Ở bài trước chắc bạn cũng đã search google được công thức tổng tự nhiên liên tiếp từ 1 tới N, bây giờ bạn hãy dùng kiến thức đó để giải quyết bài toán sau : Cho số nguyên không âm N, hãy tính các bội số của 28 mà nhỏ hơn hoặc bằng N.

Đầu vào

Số nguyên không âm N

Giới hạn

0<=N<=10^8

Đầu ra

In ra đáp án của bài toán

Ví dụ :

Input 01

60

Output 01

84

Cho 2 số N và M, hãy tìm số dư khi chia N cho M. Để tính số dư của 2 số N và M, trong trường hợp N là 1 số nguyên lớn, ta có thể dùng kiến thức toán học sau.

Bạn có N = 12345 và M = 3, bạn có thể duyệt từng chữ số của N từ trái qua phải và duy trì số dư r = 0 ban đầu, khi gặp số 1, r = r * 10 + 1, sau đó lấy r % 3 = 1, khi gặp 2, r = r * 10 + 2 = 12, r % 3 = 0,... tương tự như vậy cho tới khi gặp số cuối cùng của N, giá trị của r khi đó chính là số dư khi chia N cho M.

Đầu vào

Dòng đầu tiên là số nguyên dương N.

Dòng thứ 2 là số nguyên dương M.

Giới hạn

N có không quá 1000 chữ số

M là 1 số nguyên 64 bit.

Đầu ra

In ra kết quả của bài toán

Ví dụ :

Input 01

33067946071531150754233004290758406156224088702123385775727721812560692728127018053118203890080097807349737445483656674337750559490463284882515284188690875033135649896188928054291493979903124818899453052034828440852665076293856223903153549522293752626469246456263469220701548339620150079748958035285278459874425510146423114651458922315382153363867418189427062506833837102630904319972984364408143264207263924148697330179177840468429040754651164286732641405984220989893094158917765142342992431463840820570772383338073889397592800118784783700396465644597065301244994051135101466785516990398581
9999999999998156

Output 01

7481318352255865

Một đám đông được xếp thành N hàng, mỗi hàng có 1 số người nhất định. Nhiệm vụ của bạn là hãy tìm tên người đứng ở số thứ tự y trong hàng x.

Ví dụ người đứng ở hàng 3 số thứ tự 5 có tên là X

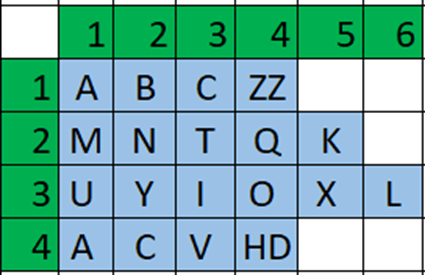
Đầu vào

Dòng 1 là N và Q tương ứng với số hàng của đám đông và số truy vấn

N dòng tiếp theo mỗi dòng mô tả 1 hàng người, trong đó số đầu tiên của 1 dòng là số người có trong hàng đó gọi là M, M từ tiếp theo là tên của M người trong hàng, tên người chỉ bao gồm 1 từ.

Q dòng tiếp theo mỗi dòng là 2 số x, y tương ứng với truy vấn

Giới hạn

1<=N,M<=10^5

1<=Q<=1000

1<=x<=N

y đảm bảo là số thứ tự phù hợp với từng hàng

Đầu ra

In ra tên người của mỗi truy vấn trên từng dòng

Ví dụ :

Input 01

8 9
5 Biden Hanh Elon Ngoc Duc 
12 Hanh Biden Thuy Thuy Duc Tim Biden Thuy Tim Lan Elon Nhung 
10 Ngoc Phuong Duc Ngoc Hanh Duc Phuong Tim Lan Lan 
10 Nhung Lan Ngoc Ngoc Biden Phuong Nhung Elon Phuong Duc 
7 Lan Elon Lan Tim Biden Ngoc Elon 
7 Phuong Hanh Lan Tim Hanh Elon Duc 
10 Hanh Hanh Biden Duc Nhung Duc Tim Elon Lan Thuy 
14 Biden Hanh Lan Duc Phuong Thuy Thuy Thuy Thuy Nhung Biden Lan Phuong Hanh 
4 10
4 9
2 5
7 7
1 4
4 3
1 1
4 7
4 3

Output 01

Duc
Phuong
Duc
Tim
Ngoc
Ngoc
Biden
Nhung
Ngoc

28Tech rất thích BTC và bây giờ anh ta nhờ bạn giúp 1 bài toán, nếu làm đúng bạn sẽ nhận được 1 BTC tương đương khoảng 64K đô la tại tháng 4/2024. Bài toán như sau : Cho xâu S có độ dài N chỉ bao gồm 3 chữ cái là B, T, C trong đó có ít nhất b chữ B, ít nhất t chữ T, ít nhất c chữ C, bạn hãy xác định có thể tồn tại bao nhiêu xâu S.

Gợi ý : Dùng vòng for lồng nhau để xét được mọi cặp thỏa mãn phương trình x + y + z = N với x >= b, y >= t và z >= c.

Bài này các bạn sử dụng kiến thức về Multinomial Coefficient. Ví dụ bài toán là cho từ mississippi, hỏi có bao nhiêu từ khác nhau có thể tạo thành bằng cách sắp đặt lại các kí tự trong từ này. Nó tương tự như đếm số cách chia n phần tử thành các tập có k1, k2, k3…km phần tử.

Ví dụ N = 4, b = 1, t = 1, c = 1 thì có tất cả 36 xâu thỏa mãn đó chính là b = 2, t = 1, c = 1 có 4! / (2! * 1! * 1!) = 12 cách b = 1, t = 2, c = 1 có 4! / (2! * 1! * 1!) = 12 cách b = 1, t = 1, c = 2 có 4! / (2! * 1! * 1!) = 12 cách

Đầu vào

Dòng 1 là T : số test case

T dòng tiếp theo mỗi dòng là 1 test gồm 4 số N, b, t, c

Giới hạn

1<=T<=1000

1<=N<=20

1<=b,t,c<=N

Đầu ra

In ra kết quả của mỗi test trên từng dòng

Ví dụ :

Input 01

5
15 4 2 1
15 6 5 3
17 3 1 7
17 1 1 11
16 6 1 6

Output 01

11043461
1411410
37925606
990624
5102240

Cho xâu ký tự S gồm các chữ số từ 0 tới 9, bạn hãy đếm số lượng xâu con liên tiếp chia hết cho 8 mà không chia hết cho 3.

Gợi ý : Dùng 2 vòng for lồng nhau để xét tất cả các xâu con, với mỗi xâu con thì tìm số dư của xâu con này vs X để xác định xem nó có chia hết cho X hay không. Lý thuyết này có ở bài tập phép chia dư Chia dư số nguyên lớn với 1 số nguyên

Bây giờ bạn chỉ cần đếm số xâu con chia hết cho 8 - số xâu con chia hết cho 24 là ra số xâu con chia hết cho 8 nhưng không chia hết cho 3.

Đầu vào

Dòng 1 là T : số test case

T dòng tiếp theo mỗi dòng là 1 test gồm xâu S

Giới hạn

1<=T<=100

S có không quá 500 chữ số

Đầu ra

In ra kết quả của mỗi test trên từng dòng

Ví dụ :

Input 01

5
9824640
13198
9412690602
5893653
25524773029

Output 01

10
1
0
3
1